Blooming fireworks with Metal and SwiftUI
Today’s inspiration I took from this post, it showcases a great fireworks animation written as a web shader.
In this article, we will explore a naive process of creating a firework effect using Metal and SwiftUI. This involves understanding the basics of shader programming and how to integrate it with SwiftUI to render dynamic animations.
We will break down the steps required to create a trail effect for the firework, including particle positioning, glow effects, and the use of trigonometric functions to simulate realistic motion.
This article is more like a further study of working with Metal rather than a guide for ready to use solution. We will face some compromises in favor of more or less optimal shader performance because of a pretty naive approach we are implementing here. You can find the source code at the end of the article.
Before writing the first line of Metal code, define the SwiftUI basis view that will be rendering the final result.
import SwiftUI
struct BloomingFirework: View {
@State private var time: Double = 0
let timer = Timer.publish(
every: 1/120,
on: .main,
in: .common
).autoconnect()
var body: some View {
let time = time
Color.black
.visualEffect { view, proxy in
view.colorEffect(
ShaderLibrary.bundle(.main)
.trailEffect(
.float(time),
.float2(proxy.size)
)
)
}
.onReceive(timer) { _ in
self.time += 0.016667
}
}
}
#Preview {
ZStack {
Color.black
BloomingFirework()
}
.ignoresSafeArea()
}Firing the trail
Since we are dealing with colorEffect, it's Metal counterpart will have a specific function signature, with pixel position and color. We also pass time parameter and canvas resolution for further animation calculation.
First step as in most cases is normalizing the pixel coordinates, in our case relative to the screen width (split by resolution.x). Thus instead of some (240, 160) pair we will be dealing with (0.8, 0.6), where the latter is agnostic to absolute values of the canvas.
Animation progress here is something that determines how fast or slow the animation will progress over time. It’s directly depends of the time clock we provide to the shader call. First, we slow down the ticks a little by dividing them by some constant. Then we extract it’s fractional part, thus the progress fluently goes from 0.0 to 1.0.
All the math behind this animation is to calculate the intensity of each pixel’s glow. For this we define intensity, it will accumulate this value during the calculations we will write a bit later.
[[ stitchable ]]
half4 trailEffect(
float2 position,
half4 color,
float currentTime,
float2 resolution
) {
float2 uv = (position - 0.5 * resolution) / resolution.x + 0.5;
float t = currentTime / 6.0;
float animationProgress = easeOutQuint(fract(t));
float intensity = 0.0;
// all the calculations here ...
return half4(half3(0.4, 0.9, 0.8) * half(min(intensity, 1.0)), 1.0);
}Implementation of the easing function is pretty straightforward, you can see more example of these functions by the link below.
float easeOutQuint(float t) {
return 1.0 - pow(1.0 - t, 5.0);
}The animation itself is divided into two steps: launching trail and burst. Keyframes approach works great here, thus we are saying that first 70% of the animation progress is the trail and last 30% for the rest.

We will work with these 70% first. The trail drawing consists of several components: the head and the particles that follow it.
Locally for this trail, its progress should also go from 0.0 to 1.0. To achieve this, we divide the progress of the entire animation by the desired duration of the trail display.
The current position of the head of the trail is the progress of overcoming the distance between the start and end point of the fireworks. For now, we will assume that this is always a straight line. Thus, to calculate the current point, we can use the standard mix function, which maps the progress to coordinates between two points.
Here we also apply a sort of optimization. If we see that the distance to the trail head is greater than 0.4 units, we simply return zero intensity for the current pixel and do not run any further logic. We’ll come back to this when we do the particle glow.
[[ stitchable ]]
half4 trailEffect(
...
) {
...
const float TRAIL_DURATION = 0.7;
float2 startPoint = float2(0.7, 0.8);
float2 endPoint = float2(0.5, 0.4);
if (animationProgress <= TRAIL_DURATION) {
float headProgress = animationProgress / TRAIL_DURATION;
float2 headPos = mix(startPoint, endPoint, headProgress);
float headDist = distance(uv, headPos);
if (headDist > 0.4) { return 0.0; }
}
return half4(half3(0.4, 0.9, 0.8) * half(min(intensity, 1.0)), 1.0);
}Next step is drawing the trail itself. It will be built with a bunch of particles. To represent them we will use for loop. We are still dealing with 0.0–1.0 range concept, here in face of normalizedIndex.
...
const int TRAIL_SAMPLES = 32;
if (animationProgress <= TRAIL_DURATION) {
...
for(int i = 0; i < TRAIL_SAMPLES; i++) {
float normalizedIndex = float(i) / float(TRAIL_SAMPLES);
}
}To position points in the trail we delay their progress based on the current head progress, but not too much. We are not deal with the points that are too far from the head — i.e. whose delayed progress is negative. Point position is calculated the exact same way we’ve did it with head.
for(int i = 0; i < TRAIL_SAMPLES; i++) {
...
float tailRelativeProgress = max(headProgress - normalizedIndex, 0.0);
if (tailRelativeProgress == 0.0) { continue; }
float2 tailPointPosition = mix(startPoint, endPoint, tailRelativeProgress);
}All that’s left for now is to get some intermediate result by determining the brightness of each pixel. The math idea here is to calculate how bright a pixel — uv - should be based on the distance from the next particle in the trail. Exponential function we use here is pretty useful when we need to get some shape be displayed but at the same time make the transition from the border of that shape to the background smooth.
for(int i = 0; i < TRAIL_SAMPLES; i++) {
...
float dist = distance(uv, tailPointPosition);
float coreGlow = exp(-dist * 100.0);
intensity += coreGlow;
}Because of the exponential function used to glow the particles we see them as a continuous line.


Right now the animation is a bit choppy, let’s fix it by adding a fade effect for some particles.
First we are going to reduce the number of particles in trail we are processing as the head progress goes to 1.0. To achieve this behavior we are multiplying the limiting TRAIL_SAMPLES value by inversed headProgress.
We also need to calculate the fade factor for the displayed particles, which is based on smoothstep function. This function maps values in some range to 0.0 - 1.0 range (again this concept, you see?)
Value stored in fadeStart is a way of specifying which farthest points should be affected by the fading effect. As this value tends to 1.0, the moment of the beginning of fade effect shifts closer to the head part of the trail.

The final value of the fade factor is also calculated using the smoothstep function, this time passing the position of the particle relative to the head part as a variable. It turns out that the closer the particle is to the head, the weaker the dimming effect. But because fadeStart is also considered dynamic, the application of the effect scales as the trail animation reaches its end point.

Here is the corresponding code part for these explanations.
for(int i = 0; i < TRAIL_SAMPLES * (1.0 - headProgress); i++) {
...
float particlePos = tailRelativeProgress / headProgress;
float fadeStart = smoothstep(0.9, 1.0, headProgress);
float fade = smoothstep(fadeStart, 1.0, particlePos);
float dist = distance(uv, tailPointPosition);
float coreGlow = exp(-dist * 100.0);
intensity += coreGlow * fade;
}
Now let’s model the sparks that follow the head. In order not to apply them for the whole trail at once, let’s say that sparks should start for those particles that pass through 0.8 of the whole trace, and then this threshold will decrease as headProgress increases. This behavior is managed by the if statement.
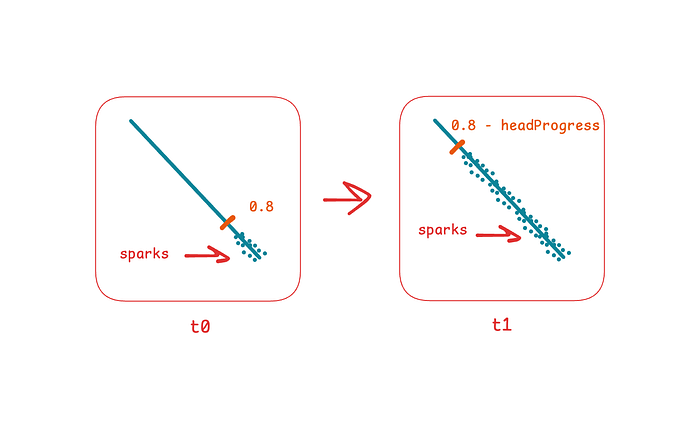
All that’s left is to create noise in the particle positions. For this purpose we will shift them vertically and horizontally by some random value with an amplitude of 0.01.
for(int i = 0; i < TRAIL_SAMPLES * (1 - headProgress); i++) {
...
if (normalizedIndex > 0.8 - headProgress) {
float noiseAmplitude = 0.01;
float noiseValue = noise(float2(float(i) * 0.5 + t * 3.0, t * 2.0)) * 2.0 - 1.0;
tailPointPosition.y += noiseValue * noiseAmplitude;
tailPointPosition.x += noiseValue * (noiseAmplitude * 2.0);
}
float dist = distance(uv, tailPointPosition);
float coreGlow = exp(-dist * 100.0);
intensity += coreGlow * fade;
}The noise function itself can be defined in any convenient way, its main task is to generate pseudo-random values, in our case from the range from 0.0 to 1.0
float noise(float2 co) {
return fract(sin(dot(co, float2(12.9898, 78.233))) * 43758.5453);
}
Let’s add a little more dynamism to the particles. To do this, it is necessary to make the glow parameter dependent on the current position of the particle and the overall progress of the animation. Thus the farther away the particle is, the sooner the exponent will go to zero and the particle will emit weaker light.
for(int i = 0; i < TRAIL_SAMPLES * (1 - headProgress); i++) {
...
float dist = distance(uv, tailPointPosition);
float coreGlow = exp(-dist * (100.0 + 200.0 * normalizedIndex * headProgress));
intensity += coreGlow * fade;
}
And add more glow around the entire print to give the impression that the surrounding area is illuminated. To apply this extra glow, we add it to the main glow rather than multiplying it. Also note that we pass the range boundaries as 0.0 and 0.4, where the upper boundary corresponds to the threshold value we used earlier to indicate that we don’t want to process pixels further than 0.4 units from the head point.
for(int i = 0; i < TRAIL_SAMPLES * (1 - headProgress); i++) {
...
float bloomGlow = rangedInverse(dist, 0.0, 0.4);
intensity += (coreGlow + bloomGlow) * fade;
}The rangedInverse function deals with scaling the value of 0.001 / x to the specified range, so the glow effect starts and finishes within this range and doesn't create any choppy visual artifacts.
float rangedInverse(float x, float minRange, float maxRange) {
float inverse = 0.001 / x;
float blendFactor = smoothstep(minRange, maxRange, x);
return inverse * (1.0 - blendFactor);
}
Before we go too far, let’s revisit the function that defines the motion direction of the trail. Right now we have it as a strait light between two points.
float2 headPos = mix(startPoint, endPoint, headProgress);Replace it with the bezier curve call.
float2 controlPoint = float2(startPoint.x, startPoint.y - 0.2);
float2 headPos = quadraticBezier(startPoint, controlPoint, endPoint, headProgress);Same for the particles in the trail, replace their position calculation.
float2 tailPointPosition = mix(startPoint, endPoint, tailRelativeProgress);With the corresponding bezier curve call.
float2 tailPointPosition = quadraticBezier(startPoint, controlPoint, endPoint, tailRelativeProgress);The quadratic bezier function is defined below. We will not consider the theory of constructing such curves, leaving this as an optional exercise.
float2 quadraticBezier(
float2 p0,
float2 p1,
float2 p2,
float t
) {
float u = 1.0 - t;
float tt = t * t;
float uu = u * u;
float2 p = uu * p0;
p += 2.0 * u * t * p1;
p += tt * p2;
return p;
}
Cloning the paths
Before we start cloning the things, let’s move the trail code into a separate function so that it can be more easily reused.
float trail(
float2 uv,
float t,
float animationProgress,
float animationDuration,
float samplesCount,
float2 startPoint,
float2 endPoint
) {
float intensity = 0.0;
float headProgress = animationProgress / animationDuration;
float2 controlPoint = float2(startPoint.x, startPoint.y - 0.2);
float2 headPos = quadraticBezier(startPoint, controlPoint, endPoint, headProgress);
float headDist = distance(uv, headPos);
if (headDist > 0.4) { return 0.0; }
for(int i = 0; i < samplesCount * (1.0 - headProgress); i++) {
float normalizedIndex = float(i) / float(samplesCount);
float tailRelativeProgress = max(headProgress - normalizedIndex, 0.0);
if (tailRelativeProgress == 0.0) { continue; }
float2 tailPointPosition = quadraticBezier(startPoint, controlPoint, endPoint, tailRelativeProgress);
float particlePos = tailRelativeProgress / headProgress;
float fadeStart = smoothstep(0.9, 1.0, headProgress);
float fade = smoothstep(fadeStart, 1.0, particlePos);
if (normalizedIndex > 0.8 - headProgress) {
float noiseAmplitude = 0.01;
float noiseValue = noise(float2(float(i) * 0.5 + t * 3.0, t * 2.0)) * 2.0 - 1.0;
tailPointPosition.y += noiseValue * noiseAmplitude;
tailPointPosition.x += noiseValue * (noiseAmplitude * 2.0);
}
float dist = distance(uv, tailPointPosition);
float coreGlow = exp(-dist * (100.0 + 200.0 * normalizedIndex * headProgress));
float bloomGlow = rangedInverse(dist, 0.0, 0.4);
intensity += (coreGlow + bloomGlow) * fade;
}
return intensity;
}Remove the code inside the declared if statement and replace it with the function call substituting required values.
if (animationProgress <= TRAIL_DURATION) {
intensity += trail(uv,
t,
animationProgress,
TRAIL_DURATION,
TRAIL_SAMPLES,
startPoint,
endPoint);
}Let’s define the last part of this fireworks display. Add a new if statement for animation progress values greater than TRAIL_DURATION. To properly track the progress of the last part, we map the animation progress to a range of 0.0 to 0.3, which corresponds to this part duration.
[[ stitchable ]]
half4 trailEffect(
...
) {
...
if (animationProgress > TRAIL_DURATION) {
float timeOffset = animationProgress - TRAIL_DURATION;
}
return half4(half3(0.4, 0.9, 0.8) * half(min(intensity, 1.0)), 1.0);
}To build firework rays, we need to get a little more of math. The burst consists of several rays that propagate along a circle whose center is the endpoint of the initial ray.
The endpoints of the rays are removed from each other by the same rotation angle, which corresponds to one segment of the circle. To get the angle value in radians, we simply divide 2Pi (360 degrees, the whole circle) by the number of rays. Hence the rotation angle of each individual ray is equal to the product of its index by the rotation angle of one segment.
We calculate the direction of the ray through the trigonometric projections of its angle of rotation. To get the end point of the ray, we move from the burst end point along the previously calculated direction by the value of the radius of this burst. In other words, we converted polar coordinates to Cartesian.

After all we call the trail function with calculated values.
const int RAYS = 8;
const float radius = 0.34;
for(int i = 0; i < RAYS; i++) {
float angle = (float(i) / float(RAYS)) * M_PI_F;
float2 direction = float2(cos(angle), sin(angle));
float2 burstEnd = endPoint + direction * radius;
intensity += trail(uv,
t,
timeOffset,
0.27,
TRAIL_SAMPLES,
endPoint,
burstEnd);
}
Counclusion
By overlaying multiple SwiftUI views containing this effect and adjusting the color calculation, you can achieve multiple fireworks displayed on the screen. But due to a less than optimal pixel processing approach, this animation can be a bit laggy.

I attach a gist with modified source code and an overlay example. In the following articles, we will try to explore ways to render more optimally and get closer to the original animation from the tweet.
upd. that following article is here:
If you liked this article, don’t forget to give it some claps so more people can see it. See you soon 🦄
